Деление на числа (оператор /)
- Когато делим две цели числа, се извършва целочислено деление и полученият резултат е цяло число с отрязана дробна част. Например 11 / 3 = 3.
- Когато делим две числа, от които поне едното е дробно, се извършва дробно деление и полученият резултат е дробно число, както в математиката. Например 11 / 4.0 = 2.75. При невъзможност за точно разделяне, резултатът се закръгля, например 11.0 / 3 = 3.66666666666667.
- Целочисленото деление на 0 предизвиква грешка по време на изпълнение (runtime exception).
- Дробното деление на 0 не предизвиква грешка, а резултатът е +/- безкрайност или специалната стойност NaN. Например 5 / 0.0 = ∞.
Ето няколко примера за използване на оператора за делене:
int a = 25;
int i = a / 4; // извършваме т.нар. целочислено деление:
// резултатът от тази операция ще бъде 6 – дробната част се отрязва,
// тъй като извършваме деление с цели числа
double f = a / 4.0; // 6.25 – дробно деление. Изрично сме указали числото 4 да се интерпретира
// като дробно, като сме добавили десетичната точка, следвана от нула
int error = a / 0; // Грешка: целочислено деление на 0
Да разгледаме и няколко примера за целочислено деление (запомнете, че при деление на цели числа в езика C# резултатът е цяло число):
Да разгледаме няколко примера за деление на дробни числа. При дробно делене резултатът винаги е дробно число и деленето никога не дава грешка и работи коректно със специалните стойности +∞ и -∞:
При отпечатването на стойностите ∞ и -∞ на конзолата може да излязат ?, защото конзолата в Windows не поддържа коректно Unicode и поврежда повечето нестандартни символи, букви и специални знаци. Горният пример най-вероятно ще изведе следния резултат:
7.5
?
-?
NaN
Съединяване на текст и число
Операторът + освен за събиране на числа служи и за съединяване на текст (долепяне на два символни низа един след друг). В програмирането съединяване на текст с текст или с число наричаме "конкатенация". Ето как можем да съединяваме текст и число с оператора +:
Забелязвате ли нещо странно? Може би очаквахте числата a и b да се сумират? Всъщност конкатенацията работи отляво надясно и горният резултат е абсолютно коректен. Ако искаме да сумираме числата, ще трябва да ползваме скоби, за да променим реда на изпълнение на операциите:
Числени изрази
В програмирането можем да пресмятаме и числови изрази, например:
var expr = (3 + 5) * (4 – 2);
В сила е стандартното правило за приоритетите на аритметичните операции: умножение и деление се извършват винаги преди събиране и изваждане. При наличие на израз в скоби, той се изчислява пръв, но ние знаем всичко това от училищната математика.
Пример1: изчисляване на лице на трапец
Да напишем програма, която въвежда дължините на двете основи на трапец и неговата височина (по едно дробно число на ред) и пресмята лицето на трапеца по стандартната математическа формула:
Ако стартираме програмата и въведем за страните съответно 3, 4 и 5, ще получим следния резултат:
3
4
5
Trapezoid area = 17.5
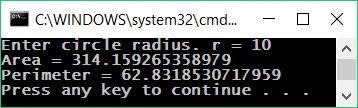
Пример2: периметър и лице на кръг
Нека напишем програма, която при въвеждане радиуса r на кръг изчислява лицето и периметъра на кръга / окръжността.
Формули:
- Лице = π * r * r
- Периметър = 2 * π * r
- π ≈ 3.14159265358979323846…
Нека изпробваме програмата с радиус r = 10:
Пример3: лице на правоъгълник в равнината
Правоъгълник е зададен с координатите на два от своите два срещуположни ъгъла. Да се пресметнат площта и периметъра му:
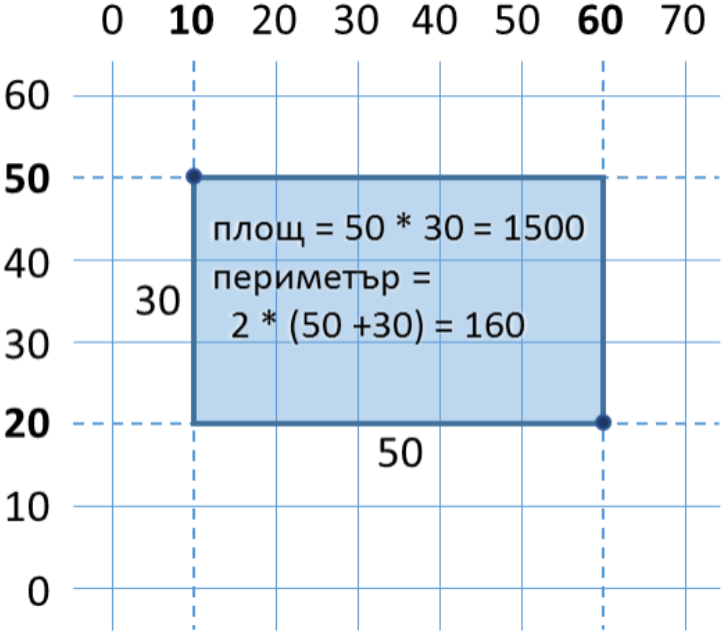В тази задача трябва да съобразим, че ако от по-големия x извадим по-малкия x, ще получим дължината на правоъгълника. Аналогично, ако от по-големия y извадим по-малкия y, ще получим височината на правоъгълника. Остава да умножим двете страни. Ето примерна имплементация на описаната логика:
Използваме Math.Max(a, b), за да намерим по-голямата измежду стойностите a и b и аналогично Math.Min(a, b) за намиране на по-малката от двете стойности.
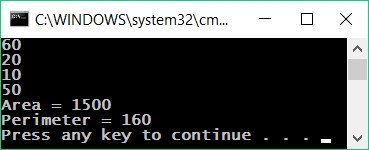
При стартиране на програмата със стойностите от координатната система в условието, получаваме следния резултат:
/. Той работи различно при цели и при дробни числа.